| |
Que signifie une pente en pourcents ? |
| |
 |
Par Franck Stevens
Article mis en ligne le 13/05/12 |
Sur les panneaux de signalisation routière ou sur les pistes de skis, l'inclinaison des pentes est généralement exprimée sous la forme d'un pourcentage plutôt que celle d'un angle. Cette notation est n'est pas toujours bien comprise et mène parfois à des malentendus.
Une pente n'est pas un angle |
On aurait par exemple tort de croire que cette valeur en pourcents correspond directement à une valeur d'angle ou qu'une pente à 100% correspond à une falaise abrupte. En réalité, la pente est définie comme une distance verticale (un dénivelé) divisée par la distance horizontale correspondante :
{$$$$}
Si à chaque fois que je parcours un mètre horizontalement sur une route, celle-ci monte de 0,10 mètre, j'aurai affaire à une route dont la pente est de 0,10, c'est-à-dire 10 pourcents :
{$$$$}
Si elle monte de 0,20 mètre pour chaque mètre parcouru horizontalement, sa pente sera de 20%, et ainsi de suite.
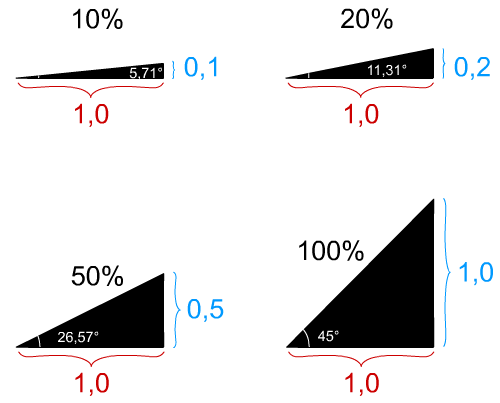
Quelques exemples de valeurs de pentes en pourcents

Quelques exemples de valeurs de pentes en pourcents
Dans le cas d'une pente à 100%, chaque mètre parcouru horizontalement correspond à une montée d'un mètre verticalement. L'angle entre la route et l'horizontale est alors de 45°, et non davantage comme on le croit parfois.
Définition de la pente d'une droite
Et les maths dans tout ça ? |
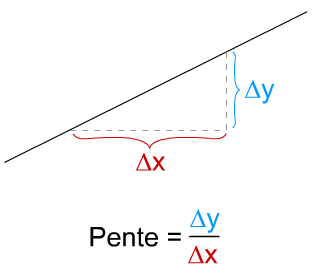
Cette définition de la pente est la même que celle qui est utilisée en mathématiques : la pente {$$ d'une droite est simplement définie comme le rapport entre une variation verticale {$$ et la variation horizontale {$$ correspondante :
{$$$$}

Définition de la pente d'une droite
Le passage entre un angle et la pente correspondante se fait grâce à la fonction tangente :
{$$$$}
Réciproquement, on peut obtenir la pente à partir de l'angle correspondant grâce à la fonction inverse, l'arctangente :
{$$$$}
Cela peut se comprendre intuitivement si on se souvient de deux choses :
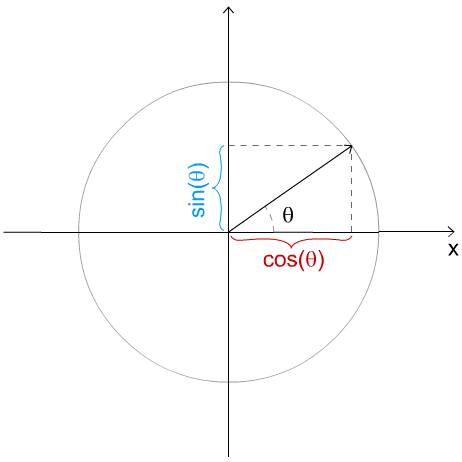
Représentation du cosinus et du sinus d'un angle sur le cercle trigonométrique
- 1) la tangente d'un angle est définie comme le rapport entre son cosinus et son sinus :
{$$$$}
- 2) sur le cercle trigonométrique, le cosinus correspond à la position horizontale d'un point tandis que le sinus correspond à sa position verticale :

Représentation du cosinus et du sinus d'un angle sur le cercle trigonométrique
Le rapport entre le sinus et le cosinus d'un angle, c'est-à-dire la tangente, correspondra donc bien à une pente.
Vous pouvez convertir une pente en angle et inversement grâce à l'outil ci-dessous :
| Pente : % |
Angle : ° |
Copyright et licence |
- Les images et vidéos utilisées sur cette page sont la propriété de leurs auteurs respectifs
- Le texte est quant à lui la propriété intellectuelle de Franck Stevens
- Vous avez le droit de reproduire ce texte à des fins non commerciales et de le modifier, à condition d'indiquer clairement vos modifications, de mentionner explicitement le nom de l'auteur et d'inclure un lien en dur vers cette page, selon les termes de la Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 3.0 non transposé.

Classement |
 Auteur(s) : Franck Stevens
Auteur(s) : Franck Stevens
 Catégorie : Question
Catégorie : Question
 Discipline(s) : Mathématiques, Géométrie
Discipline(s) : Mathématiques, Géométrie
Voir les pages... |











