La conjecture de la pizza et la difficulté de vulgariser

La communication entre le monde scientifique et le grand public n’est pas toujours facile.

Pour un chercheur, parvenir à faire parler de son travail dans la presse non-scientifique est très gratifiant, même si une publication dans un quotidien n’a aucune valeur académique en comparaison d’un article publié dans une revue scientifique. Faire parler de ses recherches dans un journal est cependant l’occasion pour le scientifique de s’assurer que le problème sur lequel il travaille peut être intéressant, même en dehors de la petite communauté des spécialistes de la question, et d’essayer de faire comprendre à ses proches à quoi il consacre ses journées.

Malheureusement, la communication entre scientifiques et journalistes est quelquefois difficile et peut engendrer beaucoup de frustration. Il n’est pas rare que les journalistes déforment involontairement les paroles des chercheurs et leur prêtent des propos scientifiquement incorrects, parfois radicalement opposés à l’idée qu’ils cherchaient à exprimer.

Pire encore, un article mal vulgarisé peut discréditer un sujet de recherche aux yeux du grand public et pousser les lecteurs à se demander comment il est possible qu’on ait payé des gens pour travailler dessus. J’aimerais illustrer ce phénomène par un exemple récent qui m’a interpelé, en retraçant les étapes de vulgarisation successives qu’a connu un article scientifique.

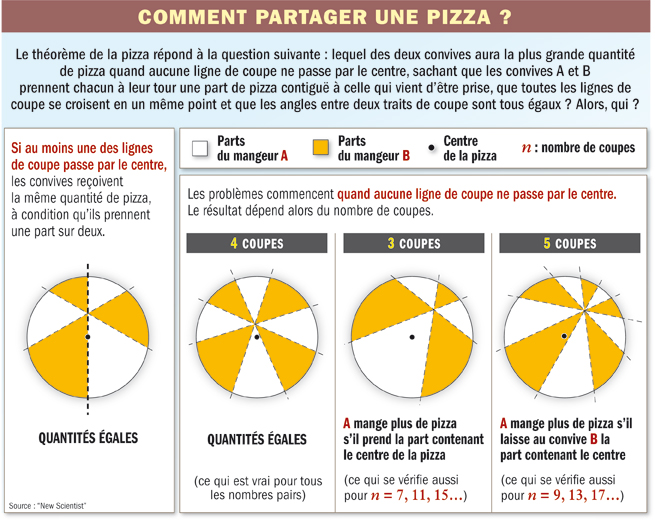
Commençons par expliquer son thème : le problème du découpage d’un disque en morceaux de surfaces égales peut paraître simple, mais il est loin de l’être dans le cas où le disque a déjà été coupé en deux selon une ligne ne passant pas par son centre. Des mathématiciens se sont penchés sur la question et ont émis une conjecture, selon laquelle il est impossible d’obtenir des morceaux de tailles égales après un nombre impair de découpes et selon laquelle le morceau qui comprend le centre du disque sera plus grand ou plus petit que les autres selon qu’il y ait eu 3, 7, 11, 15, … ou 5, 9, 13, 17, … découpes successives. Surnommée « conjecture de la pizza » en raison de l’analogie entre ce problème et celui du découpage d’une pizza, elle n’a été démontrée de façon rigoureuse que très récemment.

Deux mathématiciens américains, Rick Mabry et Paul Deiermann, en ont en effet publié une démonstration dans la revue scientifique American Mathematical Monthly en mai 2009. Pour ceux d’entre vous qui n’ont jamais eu le plaisir d’en lire, un article scientifique est habituellement un texte dense et technique présentant des résultats de recherche inédits, rédigé dans un anglais dépourvu de toute fioriture, à la mise en page standardisée et dont les seules illustrations sont souvent encadrées par des axes gradués. L’article de nos deux mathématiciens est rendu exceptionnel par la présence d’une touche d’humour dans son titre : « Du fromage et de la croûte : Une preuve de la conjecture de la pizza et autres résultats alléchants », ce qui montre que, contrairement aux reçues, les mathématiciens ont de l’humour – mais que cet humour est sensiblement différent de celui du commun des mortels.

En décembre 2009, les recherches de Mabry et Deiermann ont été le sujet d’un article dans la revue de vulgarisation britannique New Scientist. Destiné à un public de scientifiques comme de non-scientifiques, ce magazine présente les recherches de façon synthétique et simplifiée, en passant sous silence les détails techniques mais en expliquant de façon généralement fidèle la nature et les implications des résultats obtenus, le tout illustré par des graphiques faciles à interpréter. Le résultat des recherches est ainsi rendu accessible aux non-spécialistes du domaine en des termes compréhensibles pour tous les amateurs de science, cependant, un tel article est encore trop détaillé pour le grand public, qui n’aurait pas l’envie ou la patience de lire un article complet sur un sujet aussi pointu.

L’aventure des résultats des deux mathématiciens ne s’est toutefois pas arrêtée là : dans les semaines qui ont suivi, les résultats de leurs recherches ont été mentionnés sur les sites internet de journaux plus conventionnels. Cette fois, plus question de détailler les tenants et les aboutissants des recherches ou d’illustrer les articles par des graphiques : place à une description très brève du sujet de recherche, qui passe sous silence le caractère général des recherches et se concentre sur la question du découpage des pizzas, éventuellement agrémenté d’une photographie afin que les lecteurs analphabètes ou qui n’ont jamais mis les pieds dans une pizzeria puissent comprendre de quoi il est question.

Enfin, ce jeu de téléphone arabe et de simplifications successives a abouti à un article au titre éloquent :

« 11 ans de recherche pour savoir comment découper une pizza ! »

– Lu sur LePost.fr

Bien sûr, LePost.fr n’était pas un véritable journal : il s’agissait d’un site internet sur lequel des internautes motivés écrivent des articles sur des sujets d’actualité divers (et sur lequel les internautes moins motivés copient-collent le contenu d’articles publiés ailleurs). Ce titre est toutefois révélateur de la façon dont « Monsieur-tout-le-monde » a perçu les articles publiés dans la presse et de l’interprétation qu’il en a faite.

Il est rare que la presse présente des recherches de façon ouvertement négative, mais cela n’est généralement pas nécessaire pour obtenir des réactions outrées de la plupart des lecteurs : il suffit pour cela de présenter les recherches d’une façon très réductrice (« des scientifiques découvrent comment découper une pizza en parts égales ») puis de mentionner le temps ou le budget qui leur a été consacré (« les deux chercheurs ont travaillé pendant près de onze ans sur le problème »).

En lisant cela, la réaction immédiate de toute personne saine d’esprit est une juste indignation : comment peut-on payer des gens pour ce genre de recherche alors qu’il y a des enfants qui meurent de faim ? N’y a-t-il pas des sujets de recherche plus pressants, ne serait-ce que dans le domaine de la médecine ou des énergies renouvelables ? Combien de pizzas a-t-il fallu sacrifier sur l’autel de la science, aux frais du contribuable, pour aboutir à ce genre de résultats alors que le bon sens dicte que ce n’est pas très grave si une part est un peu plus petite que les autres du moment qu’il y a un peu plus de garniture dessus ?

Ce décalage entre l’article d’origine et ce que le public en retient peut à mon sens être attribué à trois phénomènes.

1) La vulgarisation abusive

Le cas de ces deux mathématiciens est intéressant puisqu’il est possible de retracer les étapes de vulgarisation successives que leur travail a subi avant d’être réduit à de l’onanisme intellectuel pour pizzaïolo obsessif-compulsif. Au fur et à mesure que l’on s’éloigne de la publication d’origine et que l’on va vers des articles destinés à un public de plus en plus large, la description des recherches des mathématiciens devient de moins en moins fidèle : au-delà d’un certain stade, il devient impossible de continuer à simplifier quelque chose sans en trahir l’esprit. Le côté technique du problème s’estompe pour céder la place à ses aspects les plus insolites, au point qu’on ne peut plus vraiment parler de vulgarisation : l’objectif n’est plus de mettre les résultats d’une recherche scientifique à la portée du lecteur mais de le distraire ou de le choquer.

2) La confusion entre le problème étudié et l’image choisie pour l’illustrer

L’un des outils les plus puissants de la vulgarisation scientifique et l’utilisation d’analogies avec des situations de la vie de tous les jours. « Découper un cercle en morceaux de surfaces égales » n’évoque pas grand-chose dans l’esprit des non-mathématiciens, mais tout le monde a déjà dû découper une pizza ou une tarte en parts égales et subir les commentaires de l’inévitable andouille qui trouve l’un des morceaux plus petit que les autres.

L’analogie est toutefois une arme à double tranchant : elle peut être nuisible si elle est poussée trop loin ou, pire, si elle est confondue avec le véritable sujet de la recherche. Ainsi, les lecteurs des articles « survulgarisés » ne réaliseront pas forcément que les pizzas n’étaient qu’un exemple et que les travaux des mathématiciens touchent un domaine plus vaste que celui de la géométrie culinaire : pour eux, des scientifiques ont consacré dix ans de leur vie à la recherche d’une méthode permettant de faire en sorte que tous les amateurs de nourriture italienne aient des parts de tailles rigoureusement identiques (mais froides, au vu de la longueur présumée des calculs préalables au découpage).

3) La difficulté de justifier la recherche fondamentale auprès d’un public non averti

On peut grossièrement diviser la recherche scientifique en deux catégories : la recherche appliquée, qui vise à résoudre des problèmes pratiques précis et même bien souvent à produire une application susceptible d’engendrer des revenus ; et la recherche fondamentale, qui n’a pas de finalité pratique et vise uniquement à accroître les connaissances humaines. Puisque la recherche fondamentale n’a pas pour but de mener de façon directe à une application quelconque, elle peut paraître « inutile » sur le court terme. Pourtant, la recherche fondamentale est essentielle au progrès de la science : une grande partie de notre technologie moderne a été rendue possible par des travaux de recherche fondamentale en physique et en mathématiques qui, à l’époque, ne semblaient pas susceptibles de mener à des applications pratiques.

Les travaux de ces mathématiciens peuvent sembler inutiles à l’heure actuelle, mais qui sait à quoi ils pourront servir demain ? Indépendamment de cela, la science doit-elle se restreindre à étudier ce qui pourrait servir ou doit-elle étudier tous les aspects du monde qui nous entoure, même ceux qui n’ont aucun intérêt pratique ?

Par cet article, je ne cherche pas à diaboliser la vulgarisation scientifique et les journalistes qui s’attaquent à cette tâche difficile. Je souhaite seulement encourager les lecteurs à réfléchir à deux fois la prochaine fois qu’ils liront un article de vulgarisation consacré au résultat de recherches apparemment absurdes. S’il existe effectivement des recherches absurdes et complètement inutiles, elles sont moins nombreuses que l’on pourrait le croire : rares sont les scientifiques qui seraient prêts à consacrer du temps et de l’énergie à un sujet s’ils le pensaient futile et plus rares encore sont les organismes disposés à financer de telles recherches.

La science se doit d’être au service de la société, une bonne communication entre le monde de la recherche et le grand public est donc essentielle. Une certaine rigueur est nécessaire pour que cette communication se fasse correctement, mais les médias l’oublient parfois et privilégient une approche sensationnaliste difficilement compatible avec une représentation fidèle de la science. Ce problème, sans conséquence grave dans le cas des recherches de ces deux mathématiciens, peut se poser plus sérieusement dans le cas des controverses scientifiques qui doivent faire l’objet de débats de société – mais ceci est un vaste sujet qui sera exploré dans un autre article…

Pour en savoir plus

• Of Cheese and Crust: A Proof of the Pizza Conjecture and Other Tasty Results (en anglais)

• Connaissez-vous le théorème de la pizza ?

Copyright et licence

• Les images et vidéos utilisées sur cette page sont la propriété de leurs auteurs respectifs
• Le texte est quant à lui la propriété intellectuelle de
• Vous avez le droit de reproduire ce texte sans modification à des fins non commerciales, à condition de mentionner clairement le nom de l'auteur et d'inclure un lien en dur vers cette page, selon les termes de la Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Pas de Modification 3.0 non transposé.

Classement

                   Auteur(s) : Franck Stevens

                   Catégorie : Article

                   Discipline(s) : Mathématiques, Philosophie des sciences, Science et société

Voir les pages...