Sciences Claires - Comment votre disque dur vous arnaque

Comment votre disque dur vous arnaque


Comment votre disque dur vous arnaque

Par Franck Stevens

Article mis en ligne le 10/08/12
Dernière mise à jour le 05 janvier 2014 à 13h28
Copyright et licence

Avez-vous déjà acheté un disque dur et constaté, en l'utilisant pour la première fois, que sa taille réelle était sensiblement plus petite que celle annoncée par le fabricant ? Avant d'appeler votre avocat, sachez que le fabricant ne vous a techniquement pas menti : il a seulement profité d'une confusion courante entre deux systèmes de préfixes d'unités. Explications.

Pour comprendre l'origine de ce problème, il faut d'abord s'intéresser à la signification de ces préfixes. En sciences, on est souvent amené à manipuler des quantités très grandes ou très petites : les atomes ont par exemple une taille de l'ordre d'un dixième de milliardième de mètre, tandis que l'univers observable mesure plus de cent millions de milliards de milliards de mètre. Il est bien entendu possible d'écrire de tels nombres normalement, mais cela les rend difficiles à lire et à reconnaître au premier coup d’œil : 0,0000000001 m ou 100000000000000000000000000 m. Difficile de travailler avec des nombres aussi petits et aussi grands écrits sous cette forme, à moins d'être prêt à passer ses journées à compter les zéros !
Scale of the Universe
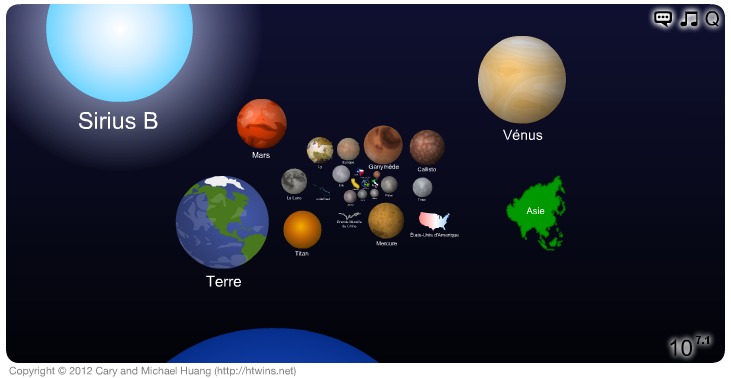
L'animation Scale of the Universe donne un bon aperçu des échelles de taille rencontrées en science
Animation : Cary Huang

Pour simplifier la notation, les scientifiques ont l'habitude d'utiliser des préfixes qui correspondent à des puissances de dix. Ils diront par exemple que la taille d'un atome est de l'ordre de 0,1 nanomètre, où le préfixe nano- signifie « 10-9 » (un dixième de milliardième). Certains de ces préfixes sont passés dans le langage courant : tout le monde sait très bien qu'un millimètre vaut un millième de mètre et qu'un kilogramme vaut mille grammes, par exemple. La liste ci-dessous reprend quelques-uns des préfixes principaux :
Préfixe Puissance de 10 Valeur
Nano- 10-9 0,000 000 001
Micro- 10-6 0,000 001
Milli- 10-3 0,001
Centi- 10-2 0,01
Déci- 10-1 0,1
Déca- 101 10
Hecto- 102 100
Kilo- 103 1000
Méga- 106 1 000 000
Giga- 109 1 000 000 000
Téra- 1012 1 000 000 000 000
Péta- 1015 1 000 000 000 000 000
Exa- 1018 1 000 000 000 000 000 000
Zetta- 1021 1 000 000 000 000 000 000 000
Yotta- 1024 1 000 000 000 000 000 000 000 000

Certains de ces préfixes, comme Méga-, Giga- et Téra-, sont désormais bien connus du grand public grâce à leur utilisation en informatique. Paradoxalement, il n'y ont pourtant pas le même sens ! Lorsque votre ordinateur parle d'un « kilooctet », il ne veut en effet pas dire « 1000 octets » mais « 1024 octets ».

Pourquoi cette différence ? Elle vient du fait qu'un ordinateur traite les informations sous la forme de nombres binaires ou bits, qui n'ont chacun que deux valeurs possibles : 0 ou 1. En conséquence, les grandeurs utilisées en informatique sont généralement des puissances de 2 : 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024...

Lors du développement des premiers ordinateurs, les informaticiens ont décidé d'utiliser le préfixe « kilo- » pour désigner 1024, puisqu'elle est raisonnablement proche de 1000. Cette tendance s'est poursuivie ensuite : un groupe de 1024 kilooctets a été appelé un mégaoctet, un groupe de 1024 mégaoctets a été appelé gigaoctets, et ainsi de suite.

Alors que le passage successif entre les préfixes kilo-, méga-, téra-, ... correspond en principe à un facteur 1000, il correspond donc à un facteur 1024 en informatique :
Facteur Valeur standard En informatique
Puissance 103 210
Valeur 1000 1024

À première vue, cette différence ne semble pas énorme : 1000 octets vaut 97,66% de la valeur octets utilisée par votre ordinateur, 1024 octets, ce qui correspond à une différence de 2,34%. La différence augmente toutefois pour les préfixes plus grands : un mégaoctet devrait en principe valoir 1000x1000 octets, c'est-à-dire 1000000 d'octets, mais il vaut 1024x1024 octets en informatique, c'est-à-dire 1048576 octets... ce qui correspond à une différence de 4,63% !
Comparaison des unités décimales et binaires
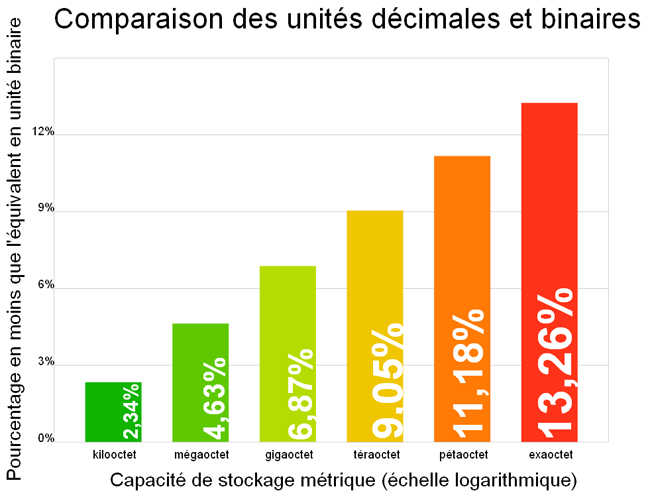
Au plus grande est la valeur à laquelle on s'intéresse, au plus grande est l'erreur commise
Image : Dirac, Licence Creative Commons

Au plus grande est la capacité de votre disque dur annoncée par le marchand, au plus grande est la différence avec la valeur réellement disponible pour votre ordinateur ! Pour éviter cette confusion, des préfixes binaires, basés sur les puissances de 2 plutôt que de 10, ont été introduits. Leurs noms sont inspirés des préfixes standards, mais leur seconde syllabe a été remplacée par bi pour indiquer leur caractère binaire :
Préfixe Puissance de 2 Valeur
Kibi- 210 1024
Mébi- 220 1 048 576
Gibi- 230 1 073 741 824
Tébi- 240 1 099 511 627 776
Pébi- 250 1 125 899 906 842 624
Exbi- 260 1 152 921 504 606 846 976
Zébi- 270 1 180 591 620 717 411 303 424
Yobi- 280 1 208 925 819 614 629 174 706 176

Ainsi, un disque dur de 1 téraoctet (valeur indiquée sur la boîte) ne peut donc en réalité contenir que 0,91 tébioctet (valeur indiquée par votre ordinateur). Le fabricant de votre disque dur ne vous a techniquement pas menti, même si cette confusion l'arrange bien : c'est votre ordinateur qui se trompe en parlant de Kilo-, Méga-, Giga-, Téraoctets là où il devrait parler de Kibi-, Mébi-, Gibi-, Tébioctets. Malheureusement, ces préfixes binaires ont encore du mal à s'imposer et commencent seulement à être utilisés par certains systèmes d'exploitation.

Pour tester par vous-même la différence entre les deux systèmes de préfixe, vous pouvez comparer les valeurs des préfixes standards et des préfixes binaires à l'aide du convertisseur ci-dessous :
est égal à


Gardez cette nuance en tête pour éviter les déceptions !


Pour en savoir plus

Définition officielle des préfixes du Système International
Prefixes for binary multiples, définition des préfixes binaires par l'International Electrotechnical Commission


Copyright et licence


Classement

                   Auteur(s) : Franck Stevens

                   Catégorie : Article

                   Discipline(s) : Informatique, Mathématiques, Arithmétique


Voir les pages...

De la plus récente à la plus ancienne            De la plus ancienne à la plus récente

Par ordre alphabétique                  Par catégories                  Par disciplines

Interviews par secteurs            Interviews par diplômes            Boîte à outils